| 研究室トップ | メンバー | 西田のページへ |
所属:京都府立大学 生命理工情報学部 理工情報学科
場所:下鴨キャンパス 2号館2階 2254号室
連絡先:y-nishida[-at-]kpu.ac.jp (西田)
| 2024.4.15 | 研究室ホームページを開設しました |
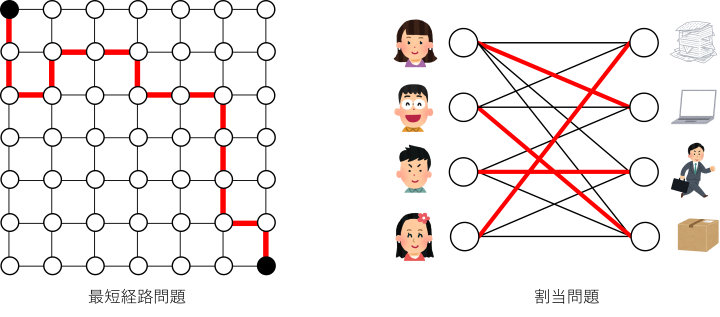
最近では,地図アプリを使えば目的地までのルートがすぐに検索できますが,どのような仕組みになっているのでしょうか. 実は,これは最短経路問題という数学の問題になっていて,効率的に計算するためのアルゴリズムが研究されています. 他にも,誰がどんな仕事をするかをうまく割り当てる問題など,身近な問題の多くは数学を用いて表すことができます. このように,与えられた問題に対して最も良い解を求める方法を考える分野を数理最適化といいます. 離散数学研究室では,この中でも特に頂点と辺からなるグラフを用いた「組合せ最適化」について,問題のモデル化やアルゴリズムの研究を行っています.

自動車の渋滞は大きな社会問題になっていますが,その原因は何なのでしょうか. こういった問題へのアプローチとして,数学を使って現象を単純化するという方法があります. 例えば,車があることを「1」,ないことを「0」で表現すると,渋滞が形成される様子を0と1の数字の変化で表すことができます. セルオートマトンとよばれるこのような単純なモデルでも,渋滞を減少させるには車間距離が重要であるという結果を得られることが数学の面白さの1つです. 研究室ではセルオートマトンを用いたモデルの解析や,0と1から連続値やベクトル値へと発展させたファジィ・セルオートマトンの研究を行っています.

上の2つのテーマは一見すると全く関係がないように見えますが,実は「max-plus代数」(あるいは「min-plus代数」)という数学的な構造が共通しています. これは,普通の意味での足し算・掛け算(とこれらの逆演算の引き算・割り算)のかわりに, 「2つの数の最大値(最小値)をとる演算」と「和をとる演算」の2つの演算で数学を構成しようというものです. このような不思議な数学の中で線形代数を考えると,最短経路問題は「行列のべき乗」,仕事の割り当ては「行列式」,セルオートマトンは「線形方程式」として表すことができ, 代数的な取り扱いが容易になります. このような背景から,研究室ではmax-plus代数での線形方程式や固有値の問題について理論的な研究を進めています.
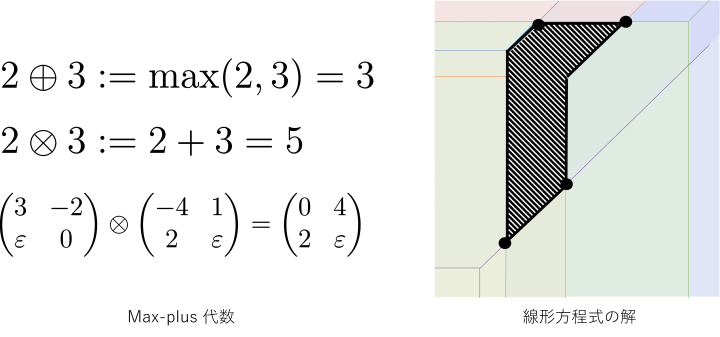
Max-plus代数上の固有値問題について解説したスライドです(2024年8月30日 第22回計算数学研究会でのチュートリアル講演より一部抜粋)