Masanori Katsuyama
EMMA(End-Members Mixing Analysis)とは?
0.降雨流出過程の解析におけるトレーサー利用(トレーサー水文学)
0.1.トレーサー水文学
水文学の課題の一つに流域における降雨流出過程,すなわち流域にもたらされた降雨が,流域内のどこを通過し,降雨に対してどのようなタイミングで,どれだけの量が流出していくか,を明らかにするという課題がある.この課題に対するひとつのアプローチとして,トレーサー(日本語では"追跡子"と訳される)を用いて水の動きを追跡する手法がある.この分野はトレーサー水文学と呼ばれる.
トレーサーは,流域内に自然に存在する物質を用いる場合と,もともと流域には存在しない(あるいは存在しても量が少ない)物質を人工的に与える場合とがある.前者の例として水の安定同位体,溶存無機・有機物質,電気伝導度(EC),水温などが上げられる.後者の例としては高濃度の食塩水,放射性同位体や蛍光塗料などが用いられる.ただし,環境への配慮などから前者の流域内にもともと存在する物質が用いられる場合が多い.
0.2.トレーサーを用いたハイドログラフの成分分離について
トレーサーを用いたハイドログラフの成分分離はこれまでに世界各地の流域で,さまざまなトレーサーを用いて行われてきている.ハイドログラフの成分分離では,渓流水は流域に存在する水の混合物であるという前提のもとに解析が行なわれ,この手法はMixing Model Approachと総称されている.Genereux and Hooper (1998)によると,トレーサーによるハイドログラフの成分分離には2つの種類がある.
0.2.1.Time-Source Separation
Time-Source Separationでは降雨時のハイドログラフを,降雨によってもたらされた"新しい水"(event water または new water)と,流域に降雨前から存在した"古い水"(pre-event waterまたはold water)に分離する(Pinder and Jones, 1969; Sklash and Farvolden, 1979)."新しい""古い"と,時間に着目するためTime-Source Separationと呼ばれる."新しい水"としては当該降雨が,"古い水"としては降雨開始前の渓流水あるいは流域に(恒常的に)存在する地下水が選択され,それぞれに含まれるトレーサー濃度と洪水流出水中の濃度,および流出水量を用いて,以下に示す質量保存則に基づいた連立方程式(Mass Balance Equations)を解くことで"新しい水""古い水"それぞれの寄与率を計算する.
-
Qo + Qn = Qt
CoQo + CnQn = CtQt
(Q:流量,C:トレーサー濃度,t:総流出水,n:新しい水,o:古い水)
各トレーサー濃度(Co,Cn,Ct)と総流出水量(Qt)が既知のため,Qo,Qnが計算される.
この2成分分離では以下の仮定を置く(Sklash and Farvolden, 1979).
- ・新しい水と古い水のトレーサー濃度は充分に異なる.
- ・新しい水のトレーサー濃度は洪水期間中一定である.
- ・洪水流出に対する土壌水の寄与は無視できるか,あるいは土壌水のトレーサー濃度は地下水のそれと等しい.
- ・くぼ地貯流水の洪水流出への寄与は小さい.
DeWalle et al. (1988)は古くから用いられている上述の2成分モデルを彼らの観測流域に適用した結果,"古い水"の割合が100%を越え,洪水流出形成をうまく説明できないとした.そして"新しい水"(降水),"古い水"(地下水)に加えて,第3の成分として土壌水を考慮する必要があるとした. (すなわち,上述の第三の仮定が満たされない)
Maule and Stein (1990),Rodhe (1998)は同位体とシリカをトレーサーに用い,渓流流出を以下の3成分に分離した(Figure 1).
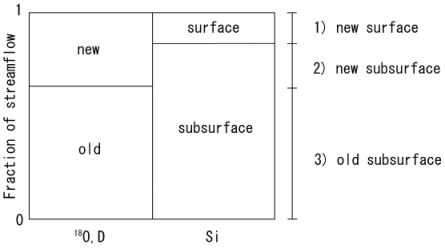
Figure 1. 18O,D,Siを用いた3成分分離(Rodhe, 1998)
- 有機物層のみを通過した新しい表層流
- 降雨中に浸透した新しい地中流
- 降雨前から存在した古い地中流
これらの分類もtime-source separationの一種であるが,どの経路を通過した水かということも意識している.
0.2.2.Geographic-Source Separation
2成分のTime-source separationでは"新しい水"と"古い水"の割合しかわからない(Genereux and Hooper, 1998).Genereux and Hemond (1990)は観測結果から"降雨中および降雨後は,全ての古い水が地下水なわけではなく,逆に全ての地下水が古い水なわけでもない"とした.水文学において重要視されるのは流出を形成している水が"新しい"か"古い"かよりも,"どこにある水が流出に寄与したか"という情報であり,このことから"Geographic-Source Separation"という概念が生じた.
1. EMMA(End-Members Mixing Analysis)について
1.1 EMMAの基礎
表流水や地下水の酸性化,汚染物質の流出などの水質問題を流域スケールで解明することの重要性が認識されている.渓流水における水質に関わる問題を解明するために,流域の流出形成の数値モデルが良く用いられる.しかし,水文過程と生物地球化学過程を合わせたモデル(水文化学モデル)においては,正しいメカニズムに沿っていない,言い換えれば正しいメカニズムを数式化することができていないため,渓流水の水文化学過程を十分に説明することは出来ていない(Hooper et al., 1990; Sklash, 1990).例えばHooper et al. (1988)は単純な6つのパラメータを持つ水文モデルでさえ,パラメータが複雑すぎる(パラメータがキャリブレーションデータから独立に決定できない)ことを示し,このようにパラメータが複雑になると水質形成機構を調べる上でモデルのパワーが低下すると指摘している.Sklash (1990)はこのようなモデル失敗の一つの大きな原因は流域に存在する水の滞留時間の推定に誤りがある,すなわちモデルで仮定されている流出経路に誤りがあることだと指摘している.これらのことから水文化学モデルにおいては,その水文学的構造をより正確に決定する必要がある.このために手法の一つとしてMixing Model Approachが用いられる.
Hooper et al. (1990), Christophersen et al. (1990)は"原位置の土壌水水質を水文化学モデルと結びつける第一段階として"(Christophersen et al., 1990),渓流水は地下水や土壌水などの流域に存在する起源となる水(source water)の混合によって形成されると仮定した上で,両者の水質を結びつける手法を示した.この手法では2種類のトレーサー濃度を軸に取り,各source waterと渓流水のトレーサー濃度をプロットした図(Mixing diagram;Figure 2)を用いて解析を行う.Mixing diagram上でsource waterの位置は渓流水が取りうる水質の最端点にあたり,渓流水はsource water を結んでできる多角形の内部にプロットされる.このことからsource waterは"端"つまり"End-Member"と呼ばれ,この解析手法は"End-Members Mixing Analysis"(EMMA)と呼ばれる.渓流水がEnd-Memberを結ぶ多角形内にプロットされない場合はEnd-Memberの選択に誤りがある.
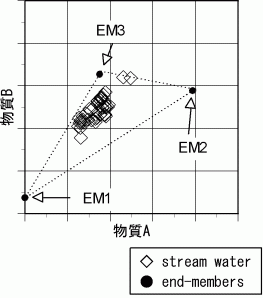
Figure.2 Mixing diagram
EMMAで用いられるトレーサーには以下の条件がある.
- 解析対象期間中に濃度変化しない
- 混合によって化学変化しない
- 異なるend-member間に十分な濃度差がある
この手法ではMixing diagramをもとに渓流流出水のハイドログラフをsource waterの寄与率に分離することが可能であり,"Geographic-Source Separation"の一手法である.EMMAは現在までに多くの研究で用いられており,多くの例でEnd-Memberの数は2または3つである(e.g., Mulholland, 1993; Ogunkoya and Jenkins, 1993; Elsenbeer et al., 1995; Ohrui and Mitchell, 1999; Hagedorn et al., 2000; 勝山ら,2000; Burns et al., 2001; Katsuyama et al.2001; Katsuyama and Ohte, 2002; 勝山ら, 2004).
Mixing diagramからハイドログラフの成分分離を行う場合は,Time-source separationの場合と同様に以下に示す質量保存則に基づいた連立方程式(Mass Balance Equations)を解く.(以下の式は3成分分離の場合)
-
f1 + f2 + f3 = 1
C[A]1f1 + C[A]2f2 + C[A]3f3 = C[A]st
C[B]1f1 + C[B]2f2 + C[B]3f3 = C[B]st
ここで,C[A]とC[B]は2種の溶存物質A,Bの濃度を,添字の1,2,3は3つのEnd-memberを,stは渓流水を,fは渓流水に寄与する各成分の寄与率を表す.
1.2. EMMAにおけるPCAの利用
EMMAを行う場合,"どの地点の水がEnd-Memberか?"と,"End-Memberの個数はいくつか?"という2点を,いかに客観的に決定するかが重要な問題である.前者はMixing diagram上に渓流水とEnd-Memberの候補をプロットし,渓流水のデータを囲み,かつ物理水文観測などの他の情報から得られた候補とをあわせて選択する.
End-Memberの個数を決定する方法として,多変量解析法の一つである主成分分析法(Principal Components Analysis;以下PCA)があわせて用いられることが多い(Christophersen and Hooper, 1992).この手法では複数の水質項目を同時に考慮することにより,渓流水を構成するEnd-Memberの必要最低限の個数を決定し(Christophersen and Hooper, 1992; Kendall et al., 1999; 勝山ら, 2004),混合プロセスをより客観的に評価することが可能になる(多田ら, 1994; Brown et al.,1999).
まず,解析対象とする渓流水に含まれるm種類の溶質濃度データセットの相関行列に対してPCAを適用し,もとのデータが持つ情報量のうち,その主成分までで説明される情報量の割合である主成分の累積寄与率を計算する.その結果,第n主成分までの累積寄与率が100%に近くなるとすれば,m次元の情報が情報量の損失がほとんどなくn次元に集約されたことになる(ただしn≦m).このn次元の空間はU空間と呼ばれる.これに対し,もとのm種類の水質データを基準化した濃度で形成されるm次元の空間はS空間と呼ばれる.
第n主成分までを考慮する場合,End-Memberはn+1個以上必要となる.Mixing diagramを作成するには,渓流水の平均濃度および標準偏差を用いて基準化したEnd-Member候補の観測濃度を,渓流水濃度データの相関行列の固有ベクトルを用いて直交変換し,U空間に投影する.このMixing diagramを元にMass Balance Equationsを解くことで,各End-Memberの寄与率が計算され,ハイドログラフの成分分離が行われる.
U空間上のEnd-Memberのデータを元のS空間へ直交変換し,End-Memberの観測値と比較することで,"理想的な"End-Memberに対して,実際のEnd-Memberのずれや,単純なMixing Modelで説明しきれない点が評価される.またEMMAの適用結果から渓流水の濃度を再現した値と,渓流水の観測値とを比較し,その再現性を見ることで,観測流域について新たな情報が必要か,判断の材料とされる(Christophersen and Hooper, 1992).
1.3. EMMAにおける誤解
1.3.1. Source or Pathway?
EMMAは前述の通り"Geographic-Source Separation"に用いられる手法であり,渓流水・河川水に寄与するSourceを決定するための手法である.つまり,渓流水は「どこにある水の混合によって形成されるか」が問われるわけであり,「どこを通った水により構成されるか」という流出経路(Pathway)は考慮されない.EMMAの原則であるEnd-Memberの独立性とは,End-Member同士の混合によって化学変化が起こらないことを意味し,流下途中で混合することがないこととは異なる.言い換えればEMMAは渓流水採取地点までの混合状態を説明するための手法であり,Sourceの水が渓流水(より厳密には渓流水採取地点)に達するまでにどの地点で混合するかは問われない.
ただし,これらの厳密な定義を踏まえた上で,SourceとPathwayは無関係なものではないため,EMMAで経路を推定するということも行われている.
1.3.2. EMMA+PCA or Only PCA?
EMMAにおいてPCAを組み合わせることの第一の目的は,渓流水を説明するために必要なEnd-Memberの個数を決定することであり,したがって第一に示すべきPCAの結果とは累積寄与率,すなわち,原データの情報全体の何パーセントまでが何番目までの主成分によって説明されるか,ということである.
一方で,流域内で得られたあらゆるサンプルの水質データにPCAを適用し,得られた結果から各主成分はどのような特徴を有することで渓流水の水質解析を行った例(Worrall et al., 2003)も見られる.
しかし,PCAをEMMAと組み合わせて用いる場合,各主成分の有する特徴を解釈することは当然可能であるが,この解釈をEnd-Memberと結びつけることは間違いである.この点に関して,Christophersen and Hooper (1992)は以下のように述べている.
"A fundamental misinterpretation in the PCA literature is the association on end-member compositions with the principle components, that is, the axes of major variation in the data."
参考文献
- Brown, V. A., McDonnell, J. J., Burns, D. A. and Kendall, C. (1999) The role of event water, a rapid shallow flow component, and catchment size in summer stormflow, J. Hydrol., 217, pp. 171-190.
- Burns, D. A., McDonnell, J. J., Hopper, R. P., Peters, N. E., Freer, J. E., Kendall, C. and Beven, K. (2001) Quantifying contributions to storm runoff through end-member mixing analysis and hydrologic measurements at the Panola Mountain Research Watershed (Georgia, USA), Hydrol. Process., 15, pp. 1903-1924.
- Christophersen, N., Neal, C., Hooper, R. P., Vogt, R. D. and Anderson, S. (1990) Modelling streamwater chemistry as a mixture of soilwater end-members - a step towards second-generation acidification models, J. Hydrol., 116, pp. 307-320.
- Christophersen, N. and Hooper, R. P. (1992) Multivariate analysis of stream water chemical data: The use of principal component analysis for end-member mixing problem, Water Resour. Res., 28, pp. 99-107.
- DeWalle, D. R., Swistock, B. R. and Sharpe, W. E. (1988) Three-component tracer model for streamflow on a small Appalachian forested catchment, J. Hydrol., 104, pp. 301-310.
- Elsenbeer, H., Lorieri, D. and Bonell, M. (1995) Mixing model approaches to estimate storm flow sources in an overland flow-dominated tropical rain forest catchment, Water Resour. Res., 31, pp. 2267-2278.
- Genereux, D. P. and Hemond, H. F. (1990) Three-component tracer model for stormflow on a small Appalachian forested catchment - comment, J. Hydrol., 117, pp. 377-380.
- Genereux, D. P. and Hooper, R. P. (1998) Oxygen and hydrogen isotopes in rainfall-runoff studies, Isotope tracers in catchment hydrology, Kendall, C. and McDonnell, J. J. (Eds.), Elsevier, Amsterdam, pp. 319-346.
- Hagedorn, F., Schleppi, P., Waldner, P. and Fluhler, H. (2000) Export of dissolved organic carbon and nitrogen from Gleysol dominated catchments - the significance of water flow paths, Biogeochem., 50, pp. 137-161.
- Hooper, R. P., Stone, A., Christophersen, N., Grosbois, E. D. and Seip, H. M. (1988) Assessing the Birkens Model of Stream Acidification Using Multisignal Calibration Methodology, Water Resour. Res., 24, pp. 1308-1316.
- Hooper, R. P., Christophersen, N. and Peters, N. E. (1990) Modelling streamwater chemistry as a mixture of soilwater end-members - an application to the Panola Mountain catchment, Georgia, U.S.A, J. Hydrol., 116, pp. 321-343.
- 勝山正則,大手信人,内田太郎,浅野友子,木本秋津 (2000) 降雨流出過程の相違が渓流水質形成機構に与える影響, 水文・水資源学会誌, 13, pp. 227-239.
- Katsuyama, M., Ohte, N. and Kobashi, S. (2001) A three-component end-member analysis of streamwater hydrochemistry in a small Japanese forested headwater catchment, Hydrol. Process., 15, pp. 249-260.
- Katsuyama, M. and Ohte, N. (2002) Determining the sources of stormflow from the fluorescence properties of dissolved organic carbon in a forested headwater catchment, J. Hydrol., 268, pp. 192-202.
- 勝山正則,大手信人,小杉賢一朗 (2004) 風化花崗岩山地源流域の渓流水NO3-濃度形成に対する水文過程のコントロール, 日林誌86, pp. 27-36.
- Kendall, K. A., Shanley, J. B. and McDonnell, J. J. (1999) A hydrometric and geochemical approach to test the transmissivity feedback hypothesis during snowmelt, J. Hydrol., 219, pp. 188-205.
- Maule, C. P. and Stein, J. (1990) Hydrologic flow path definition and partitioning of spring meltwater, Water Resour. Res., 26, pp. 2959-2970.
- Mulholland, P. J. (1993) Hydrometric and stream chemistry evidence of three storm flowpaths in Walker Branch Watershed, J. Hydrol., 151, pp. 291-316.
- Ogunkoya, O. O. and Jenkins, A. (1993) Analysis of storm hydrograph and flow pathways using a three-component hydrograph separation model, J. Hydrol., 142, pp. 71-88.
- Ohrui, K. and Mitchell, M. J. (1999) Hydrological flow paths controlling stream chemistry in Japanese forested watersheds, Hydrol. Process., 13, pp. 877-888.
- Pinder, G. F. and Jones, J. F. (1969) Determination of the ground-water component of peak discharge from the chemistry of total runoff, Water Resour. Res., 5, pp. 438-445.
- Rodhe, A. (1998) Snowmelt-dominated systems, Isotope tracers in catchment hydrology, Kendall, C. and McDonnell, J. J. (Eds.), Elsevier, Amsterdam, pp. 391-433.
- Sklash, M. G. and Farvolden, R. N. (1979) The role of groundwater in storm runoff, J. Hydrol., 43, pp. 45-65.
- Sklash, M. G. (1990) Environmental isotope studies of storm and snowmelt runoff generation, Process studies in hillslope hydrology, Anderson, M. G. and Burt, T. P. (Eds.), John Wiley and Sons, Chichester, pp. 401-436.
- 多田明夫,堀野治彦,渡辺紹裕,丸山利輔 (1994) PCAを用いた流出成分分離による水質形成機構の推定 -造成農地の水質形成機構の研究(Ⅰ)-, 農業土木学会論文集, 174, pp. 49-55.